Eşitsizlikler 2009 KPSS Soru ve Çözümü

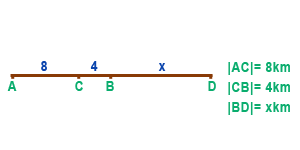
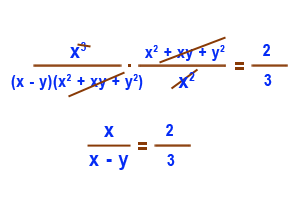SORU:

(2x - 1)(-x + 5)

        x - 3

≥ 0
Eşitsizliğinin çözüm kümesi,

1. x ≤ 1/2
2. 1/2 ≤ x ≤3
3. 3 < x ≤ 5
4. x ≥ 5

kümelerinden hangilerinin birleşimi ile oluşmuştur?(2009 KPSS)

A) Yalnız II   B) Yalnız III   C) I ve III   D) I ve IV   E) II ve IV

ÇÖZÜM:

(2x - 1)(-x + 5)

        x - 3

≥ 0

Yukarıdaki eşitsizlikte ilk olarak eşitsizliğin değerini sıfır yapan sayılar bulunmalıdır. Bunun için eşitsizliği oluşturan çarpanlar tek tek sıfıra eşitlenir.

2x - 1 = 0 => x = 1/2
-x + 5 = 0 => x = 5
x - 3 = 0 => x = 3 Burada x = 3 değerini alamaz.

Sayı

Sıfır

= ∞ belirsizliği meydana gelir

Bulduğumuz x değerleri için eşitsizliğin tablosu aşağıda oluşturulmuştur. Eşitsizliği sıfır yapan değerler işaretlenmiştir.

Soruda verilen eşitsizlik denkleminde x ≥ 0 şartı var. Bu bilgiye istinaden eşitsizlik için verilen x değerlerine karşılık denklemin alabileceği işaret değerleri + ve - şeklinde belirtilmiştir. Bizim çözüm kümemiz ise eşitsizlik denklemi için ≥ 0 şartını sağlayan sayılardır. Bu sayı aralıkları sarı renkle işaretlenmiştir. X = 3 değerini alamayacağından dolayı kırmızı çizgilerle sınırlandırılmıştır. Buna göre çözüm kümesi elemanları,

x ≤ 1/2 ve 3 < x ≤ 5 şeklindedir. Çözüm kümemiz ise;

Çözüm Kümesi = (x ≤ 1/2) U (3 < x ≤ 5) dir.

Doğru Cevap C Seçeneğidir.



Turgut Arslan

Rasyonel Sayılar 2009 KPSS Soru ve Çözümü

SORU:

Olduğuna göre, x/y kaçtır?(2009 KPSS)

A) -3   B) -2   C) -1   D) 2   E) 3

ÇÖZÜM:

Rasyonel denklemler çözülürken, aritmetiksel işlemler rasyonel sayılarda olduğu gibi yapılır. İki rasyonel sayı birbirlerine bölünürken bölünen olduğu gibi kalırken bölen yani payda kısmı ters çevrilip bölenle yani pay kısmı ile çarpılır. sorudaki,

x3 - y3 ifadesi yani iki küp farkı açık şekilde yazılmıştır.

x3 - y3 = (x - y)(x2 + xy + y2)

gerekli sadeleştirmeler yapılır ve yukarıdaki eşitlik elde edilir. Ardından içler dışlar çarpımı yaılırsa,

3x = 2(x - y)

3x = 2x - 2y

x = -2y

x/y = -2 olarak bulunur.

Doğru Cevap B Seçeneğidir.

Turgut Arslan

Analitik Geometri 2009 KPSS Soru ve Çözümü

SORU:

Yukarıdaki dik koordinat sisteminde K(4,3) noktasından geçen doğru x eksenini apsisi a olan, y eksenini de ordinatı b olan noktalarda kesmektedir.
Buna göre (a - 4)(b - 3) çarpımının değeri kaçtır?(2009 KPSS)

A) 8   B) 12  C) 14  D) 16  E) 18

ÇÖZÜM:

Öncelikli olarak genel doğru denklemini yazalım.

   x  

x1 - x0

+

   y  

y1 - y0

= 1
Grafikteki verileri kullanarak doğru denklemimizi oluşturalım,

   x  

a - 0

+

   y  

b - 0

= 1
fizikliblog.blogspot.com

x

a

+

y

b

= 1 şimdi de paydaları eşitleyelim ve gerekli işlemleri yapalım
(b)    (a)
4b + 3a = ab olur. buradan,
ab - 4b - 3a = 0 bulunur.
(a - 4)(b - 3) Soruda verilen çarpım işlemini yaparsak,
ab - 4b - 3a + 12 elde edilir. burada yukarıda bulduğumuz ifadeyi yerine koyarsak,
0 + 12 = 12 olarak bulunur.
Doğru Cevap B Seçeneğidir.



Turgut Arslan

Geometri 2009 KPSS Soru ve Çözümü

SORU:

Yukarıdaki verilere göre x kaç cm'dir?(2009 KPSS)

A) 4 -    3   B) 3 -    2   C) 2 +    3   D) 2 +    2   E) 1 +    3

ÇÖZÜM:

İlk önce E noktasından |AB| kenarına bir dik çizilir. EHB dik üçgeni elde edilir. EHB üçgeni bir 30 - 60 - 90 üçgenidir. Bir özel üçgendir. |EH| ile |CB| paraleldir. HEB açısı ile CBE açısı iç ters açılardır ve birbirlerine eşittir. Böylece CBE açısı 30 derece olarak bulnur. CEB üçgeni de bir özel üçgen çeşidi olan 30 - 60 - 90 üçgenidir. Bu üçgenlerde 30 derecenin karşısınıdaki kenar hipotenüsün yarısıdır. Burada hipotenüs |CB| kenarıdır. Buna göre |CE| = 2 cm, |BE| = 2    3 bulunur. |BE| kenarı EHB üçgeninin hipotenüsüdür. Aynı kuralı bu üçgen için de işletirsek,
|HB| =    3 cm bulunur.Buradan hareketle,

4 = x +    3

x = 4 -    3 cm bulunur.

Doğru Cevap A Seçeneğidir.

Turgut Arslan

Pisagor Teoremi 2009 KPSS Soru ve Çözümü

SORU:

Aşağıdaki şekilde uç noktaları A ve D olan bir su bitkisinin durgun [OA] ve rüzgarlı havadaki [OD] konumu gösterilmiştir.

Buna göre x cm'dir?(2009 KPSS)

A) 25   B) 28   C) 30   D) 32   E) 35

ÇÖZÜM:

İlk olarak bitkinin boyunu hesaplayalım
|OA| = x + 5cm
aynı şekilde
|OD| = x + 5cm (bitkinin boyu sabittir.)
|OC| = |OD| - |CD|
|OC| = x + 5 - 3 = x + 2
OBC dik üçgeninde Pisagor Teoremi uygulanırsa,
x2 + 122 = (x + 2)2
x2 + 122 = x2 + 4x + 4
4x + 4 = 144
4x = 140
x = 35 cm bulunur.
Doğru Cevap E Seçeneğidir.



Turgut Arslan

Hareket Problemleri 2009 KPSS Soru ve Çözümü

SORU:

Şekildeki A B noktalarından aynı anda hareket eden iki araç, birbirlerine doğru hareket ettiklerinde C noktasında karşılaşıyorlar. Aynı yönde hareket ettiklerinde biri diğerine D notasında yetişiyor.

Buna göre x kaçtır?(2009 KPSS)

A) 8   B) 12   C) 13   D) 15   E) 16

ÇÖZÜM:

A'dan hareket dnle B'den hareket den araçlar aynı anda(t kadar sürede) C noktasında karşılaşıyorlar. Aynı süre içinde A'dan gelen 8km, B'den gelen ise 4km yol kat ettiğine göre A'daki araç B'dekinin iki katı hıza sahiptir.

Yol = Hız . Zaman

fizikliblog.blogspot.com VA = 2V

VB = V olur. Buna göre B'den çıkan ve D yönünde hareket eden araç t sürede,

(1)    x = V.t kadar yol alır.

Aynı şekilde A'dan çıkan ve D yönünde hareket eden araç ise x + 12km yol alır. Bu aracın aldığı yol denklemi ise,

(2)    x + 12 = 2V.t olur

Bu denklemde x yerin V.t eşitliği yazılırsa,

Vt + 12 = 2Vt

Vt = 12 olur.

 (1) denklemindeki eşitliğe bakarsak,

x = V.t den x = 12km bulunur.

Doğru Cevap B Seçeneğidir.

Turgut Arslan

Rasyonel Sayılar 2009 KPSS Soru ve Çözümü

SORU:

Belirli bir yükseklikten bırakılan bir top, yere vuruşundan sonra bir önceki yüksekliğin 3/8'i kadar yükselmektedir.

Top yere ikinci vuruşundan sonra 108 cm yükseldiğine göre birinci vuruşundan sonra kaç cm yükselmiştir?(2009 KPSS)

A) 160   B) 162   C) 168   D) 204   E) 288

ÇÖZÜM:

Topun başlangıçtaki yüksekliği x cm olsun, Top yere vurduktan sonra 1. yükselişinde 3x/8 cm yükselir. 2. vuruşundan sonra ise 9x/64 cm yüksekliğe ulaşır.

9x/64 = 108

9x = 108 . 64

x = 768 bulunur. Bu topun başlangıçtaki yüksekliğidir. Birinci vuruştan sonraki yüksekliği ise bunun 3/8'i olur ve,

1. vuruştan sonraki yükseklik = 3 . 768 / 8

1. vuruştan sonraki yükseklik = 288 cm bulunur.

Doğru Cevap E Seçeneğidir.

Turgut Arslan

Olasılık 2009 KPSS Soru ve Çözümü

SORU:

3 ü kız 4 ü erkek olan bir grup yan yana oturacaktır.

Bu oturumda 3 kız öğrencinin yan yana bulunma olasılığı kaçtır?(2009 KPSS)

A) 1/7   B) 2/7   C) 3/7   D) 4/7   E) 5/7

ÇÖZÜM:

Hiçbir şart öne sürülmeseydi toplamda 7 kişi olan bu gruptaki elemanlar 7! farklı şekilde oturabilirlerdi. 3 kız yan yana kendi aralarında 3! farklı şeklide oturabilir. 4 erkekle birlikte 3 lü kız grubunu da bir kişi kabul edersek bu durumda sanki 5 kişi varmış gibi düşünebiliriz(kızlar birbirlerinden ayrılmadıkları için) bu durumda bu 5'li grup kendi aralarında 5! farklı şekilde oturabilir. Kızların kendi aralarındaki oturma kombinasyonunu da hesaba katarsak toplamda 7 kişi kızlar beraber olmak koşuluyla

5! . 3!

farklı şekilde oturabilir. Bu durumda kızların yan yana bulunma olasılığı,

(5! . 3!) / 7! = ( 5 . 4 . 3 . 3! ) / 7 . 62 . 5 . 4 . 3!

Sonuç = 1 / 7 olarak bulunur. 

Doğru Cevap A Seçeneğidir.

Turgut Arslan

Hareket Problemleri 2009 KPSS Soru ve Çözümü

SORU:

Bir deniz motoru |AB| yolunu saatte (v + 20)km hızla 24 dakikada, aynı yolu saatte (v - 6)km hızla 32 dakikada alıyor.
Buna göre |AB| yolu kaç km'dir?(2009 KPSS)
A) 40,2   B) 40,8   C) 41,2   D) 41,6   E) 41,8

ÇÖZÜM:

|AB| yolu x km olsun, soruda hızlar saat cinsinden verildiği için dakikaları saate çevirelim
60 dakika 1 saat ise
24 dakika y saat eder (Doğru orantı)

60y = 24
y = 24/60 = 2/5 saat

60 dakika 1 saat ise
32 dakika y saat eder (Doğru orantı)

60y = 32
y = 32/60 = 8/15 saat

Yol = Hız . Zaman Formülünden yola çıkarak x km için iki farklı ifade yazılabilir.

x = (v + 20). 2/5
x = (v - 8) . 8/15

(v + 20). 2/5 = (v - 8) . 8/15
(v + 20) = (v - 8). 4/3 buradan,
6v + 120 = 8v - 48
2v = 168
v = 84 km/h olur.
Bu değeri x için yazılan denklemlerden birinde yerine koyarsak |AB| yolunu hesaplayabiliriz
x = (84 + 20). 2/5
x = 41,6 km bulunur.

Doğru Cevap D Seçeneğidir.



Turgut Arslan

Oran Orantı 2009 KPSS Soru ve Çözümü

SORU:

Sıfırdan büyük a, b, c sayıları sırasıyla 2, 4, 6 sayıları ile orantılı ve,
b2 = a + c
olduğuna göre a + b + c toplamı kaçtır?(2009 KPSS)
A) 5   B) 6   C) 7   D) 8   E) 10

ÇÖZÜM:

a, b, c  sayıları 2, 4, 6 ile orantılı ise k orantı sabiti olmak üzere bu sayılar için,
a = 2k  b = 4k  c = 6k  yazılabilir. bu sayılar,

b2 = a + c ifadesinde yerine yazılırsa,
(4k)2 = 2k + 6k olur
16k2= 8k
k = 1/2 bulunur. Artık orantı sabitini bulduğumuza göre a, b ve c sayılarını hesaplayabiliriz.

a = 2 . 1/2 = 1   b = 4 . 1/2 = 2    c = 6 . 1/2 = 3 buna göre

a + b + c = 1 + 2 + 3 = 6 bulunur.

Doğru Cevap B Seçeneğidir.



Turgut Arslan

İşlem ve Modüler Aritmetik 2009 KPSS Soru ve Çözümü

SORU:

A = {a, b, c, d, e} kümesi aşağıda verilen * işlemi ile bir değişmeli grup oluşturmaktadır.

Her x * A için bir fx fonksiyonu
fx(y) = x-1 * y ∈ A biçiminde tanımlanıyor.
Buna göre, fe(fb(e)) aşağıdakilerden hangisine eşittir?(2009 KPSS)
A) a   B) b   C) c   D) d   E) e

ÇÖZÜM:

 Öncelikli olarak soruda tanımlanan * işleminin birim elemanını bulmalıyız. Birim eleman kendisi ile işleme girildiğinde sonucu değiştirmeyen elemandır.

Yukarıdaki tabloda işaretli olan c elemanı kendisi ile yapılan * işleminin sonucunu değiştirmemektedir. Bu sebepten dolayı * işleminin etkisiz elemanıdır.
b-1 = d (d, b ile * işlemine girip birim eleman olan c'yi verdiği için b'nin tersi olur.)
e-1 = a (a, e ile * işlemine girip birim eleman olan c'yi verdiği için e'nin tersi olur.)
fe(fb(e)) = fe(b-1 * e) = fe(d * e)
fe(a) = e-1 * a = a * a = d olur

Doğru Cevap D Seçeneğidir.



Turgut Arslan  

Köklü Sayılar 2009 KPSS Soru ve Çözümü

SORU:

a bir gerçel sayı olmak üzere,
(2 -   2a + a2). (a +   2 ) = 2  2 - 8
olduğuna göre a kaçtır?(2009 KPSS)
A) -2   B) -1   C) 0   D) 1   E) 2

 ÇÖZÜM:

(2 -   2a + a2). (a +   2 ) = 2  2 - 8
2a -   2a2 + a3 + 2  2 - 2a +   2a2 = 2  2 - 8
2  2 + a3 = 2  2 - 8
a3 = - 8
a3 = (- 2)3
a = -2 bulunur.

Doğru Cevap A Seçeneğidir.



Turgut Arslan

İşçi ve Havuz Problemleri 2009 KPSS Soru ve Çözümü

SORU:

x sayıda işçinin 10 günde 10 saat çalışmasıyla 15 günde bitirilebilen bir iş, işçi sayısı artırılarak ve günde 8 saat çalışılarak 12 günde bitirilebiliyor.

Buna göre x aşağıdakilerden hangisi olabilir? (2009 KPSS)

A) 10   B) 12   C) 18   D) 24   E) 32

ÇÖZÜM:

İşçi ve havuz problemlerinin çözümünde, hesaplamalar bahis geçen olayın(bir işin yapılması ya da havuzun dolması-boşalması gibi ) gerçekleşmesi için haracanan toplam zaman üzerinden yapılır. Bu soruda ilk önce; işçi sayısı, işin yapılması için geçen gün sayısı ve günlük çalışma süresi çarpılırsa, harcanan toplam mesai bulunur

x işçi 10 saat  15 gün (x işçi toplamda 10 . 15 . x = 150x saat mesai harcar)

y işçi 8 saat    12 gün (y işçi toplamda 8 . 12 y = 96y saat mesai harcar)

                                   

Her iki durumda da aynı iş yapıldığından dolayı, bu iki durumun birbirlerine oranı 1 olur. Yani

150x / 96y = 1

150x = 96y

      x = (96/150)y

      x = (16/25)y olur. (1)

Soruda işçi sayısının artırıldığından bahsediliyor. Bu durmda  x < y'dir. x'in durumunun daha iyi değerlendirilebilmesi için (1) ifadesini biraz değiştirelim,

x / y = 16 / 25 (2)

(2) ifadesinde de görüldüğü gibi x, 16 sayısı ile orantılıdır. Yani x 16'nın bir katı ve 25'ten de küçüktür(y'den dolayı). Bu durmda

x = 32 olabilir.

Doğru Cevap E Seçeneğidir.



Turgut Arslan

Kümeler 2009 KPSS Soru ve Çözümü

SORU:

32 kişinin katıldığı bir sınavda her bir öğrenci matematik ya da fen testlerinden en az birini yapmıştır. Yalnız matematik testini yapan öğrenci sayısı fen testini yapan öğrenci sayısının 2 katında 4 eksiktir.

Buna göre yalnız matematik testini yapan öğrenci sayısı kaçtır?(2009 KPSS)

A) 12   B) 14   C) 16   D) 18   E) 20

ÇÖZÜM:

Öncelikli olarak Matamatik ve Fen kümelerini oluşturmalıyız. Matematik ve Fen testlerini çözen öğrencilerin oluşturdukları kümeleri soruda verilen ipuçlarına uygun bir şekilde çizelim,

Grafikte yalnız Fen testini çözen öğrencilerin sayısına x dersek, soruda verilen şarta bağlı olarak Matematik testini çözen öğrenci sayısı; 2x - 4 olur. Sınıf mevcudu 32 olarak verilmişti. Buna göre denklemimiz,

2x - 4 + x = 32

3x = 32 + 4

3x = 36

x = 12 Burada bulduğumuz Fen testini çözen öğrenci sayısıdır. Matematik testini çözen öğrenci sayısı iki yoldan bulunabilir.

1. Yol:

 Sınıf mevcudundan Fen testini çözen öğrenciler çıkarılır.

32 - 12 = 20

2. Yol

Bulunan x değeri denklemde yerine yazılır.

2(12) - 4 = 24 - 4 = 20 Bulunur.

Doğru Cevap E Seçeneğidir.

Turgut Arslan

Rasyonel Sayılar 2009 KPSS Soru ve Çözümü

SORU:

a2 - b2 = 16

  1   

a + b

+

  1  

a - b

=

 17 

16

olduğuna göre a kaçtır?(2009 KPSS)
A) 13/2   B) 15/2   C) 17/2   D) 19/4   E) 21/4

ÇÖZÜM:

  1   

a + b

+

  1  

a - b

=

 17 

16

denklemin sol tarafında paydalar eşitlenir
(a - b)         (a + b)

 a - b 

a2 - b2

+

 a + b 

a2 - b2

=

 17 

16

a - b + a + b

    a2 - b2

=

 17 

16

  2a  

a2 - b2

=

 17 

16

a2 - b2'in değeri yerine yazılırsa

  2a  

  16

=

 17 

 16

2a = 17

a = 17/2 bulunur.

Doğru Cevap C Seçeneğidir.



Turgut Arslan  

OBEB ve OKEK 2009 KPSS Soru ve Çözümü

SORU:

a ve b birer pozitif tam sayı olmak üzere,
ekok(a,b) = 2.32
olacak şekilde kaç farklı (a,b) sıralı ikilisi vardır?(2009 KPSS)
A) 6   B) 12   C) 13   D) 14   E) 15

ÇÖZÜM:

Bu soruda aslına ekok değeri 2.32 olan a ve b sayıları sorulmaktadır. a ve b birer Z+ olmak üzere ekok değeri yukarıdaki gibi olan (a,b) sıralı ikilileri sırasıyla;

(a,b) = (1, 18)
(a,b) = (2, 9)
(a,b) = (2, 18)
(a,b) = (3, 18)
(a,b) = (6, 9)
(a,b) = (6, 18)
(a,b) = (9, 18)
(a,b) = (18, 1)
(a,b) = (9, 2)
(a,b) = (18, 2)
(a,b) = (18, 3)
(a,b) = (9, 6)
(a,b) = (18, 6)
(a,b) = (18, 9)
(a,b) = (18, 18) olmak üzere 15 adettir.

Doğru Cevap E Seçeneğidir

Üslü Sayılar 2009 KPSS Soru ve Çözümü

SORU:

3 . 9x + 1

27x + 1

=

 1 

9

olduğuna göre x kaçtır?(2009 KPSS)
A) 3   B) 2   C) 1   D) -1   E) -2

ÇÖZÜM:

3 . (32)x + 1
(33)x + 1

=

 1 

32

3 . 32x + 2

33x + 3

=

 1 

32

32x + 3

33x + 3

=

 1 

32

32x + 3 - 3x -3 = 3-2

3-x = 3-2 eşitliğin iki tarafındada tabanlar aynı olduğundan üsler birbirlerine eşittirler.

-x = -2

x = 2 bulunur. Doğru Cevap B Seçeneğidir.



Turgut Arslan

Köklü Sayılar 2009 KPSS Soru ve Çözümü

SORU:

   5 -    21 ifadesi aşağıdakilerden hangisine eşittir? (2009 KPSS)

A)

   7 -    3

   2

B)

   5 -    3

   2

C)

   7 -    5

   3

D)

   5 +    3

   3

E)

   5 +    7

   3

ÇÖZÜM:

   5 -    21 ifadesinde pay ve paydayı    2 ile çarparak genişletelim.

   2 . (   5 -    21)

   2

=

   10 - 2   21

   2

   (7 + 3) - 2   (7 . 3)

   2

=

   7 -    3

   2

olarak bulunur.

Doğru Cevap A Seçeneğidir.



Turgut Arslan

Karışım Problemleri 2009 KPSS Soru ve Çözümü

SORU:

Tuz oranı %20 olan tuzlu sudan 30 lt su buharlaştırılırsa yeni tuz oranı %30 oluyor.
Buna göre başlangıçtaki tuzlu su miktarı kaç litredir?(2009 KPSS)
A) 120   B) 100   C) 90   D) 80   E) 60

ÇÖZÜM:

Başlangıç için kabımızda x litre tuzlu su olsun. Bu tuzlu suyun %20'si tuz olduğuna göre başlangıç olarak kabımızda (20/100)x lt  kadar tuzumuz var demektir.

Şimdi kaptan 30 lt su buharlaştıralım. Bu durumda kabımızdaki tuzlu su miktarı x - 30 lt olur. Tuz su ile birlikte buharlaşmayacağı için kapta kalır. Yani karışımdaki tuz miktarı değişmez.

Tuz oranı = Tuz Miktarı / Karışımın Hacmi

Karışımdaki tuz yüzdesini(oranını) hesaplamak için karışımdaki tuz miktarını tüm karşımın hacmine böleriz. 30 lt su buharlaştırdığımız zaman karışımın tuz yüzdesi %30 oluyordu. Bu ipucunu kullanarak çözüme varabiliriz. Başlangıçta karışımda (20/100)x kadar tuzumuz vardı. Buharlaştırılmadan sonra tuz miktarı aynı kaldı.Buna göre denklemimiz

Yeni tuz oranı = (30 / 100) = (20/100)x /( x - 30)   (Gerekli sadeleştirmeler yapılırsa,)
2x = 3x - 90
x = 90 lt bulunur.

Doğru Cevap C Seçeneğidir.


Turgut Arslan

Mutlak Değer 2009 KPSS Soru ve Çözümü

SORU:

x ∈ R ve x<1/4 olmak üzere,
|3x - |x -1|| - 2
ifadesinin eşiti aşağıdakilerden hangisidir?(2009 KPSS)
A) -4x - 3   B) -4x - 1   C) 4x - 3   D) 4x + 1   E) 4x + 3

ÇÖZÜM:

Öncelikli olarak |x - 1| ifadesinin mutlak değer dışına nasıl çıkması gerektiğini bulmalıyız.
soruda verilen x < 1/4 şartında eşitsizliğin her iki tarafından 1 çıkaralım.
x - 1 <1/4 - 1
x - 1 < - 3/4 olarak bulunur. Bu |x - 1| mutlak değerinin içinin negatif olduğunu gösterir. Negatif sayıların mutlak değerini bulmak için -1 ile çarparız. Buna göre ,
|x - 1| = -1.(x - 1) = 1 - x  olur.  Bulduğumuz bu değeri soruda verilen ifade içindeki yerine yazalım.
|3x - (1 - x)| - 2 = |3x -1 + x| - 2
|4x - 1| - 2  (1)
Şimdi bu ifadede mutlak değerin durumunu öğrenebilmemiz için 4x'i incelememiz gerekir.
Soruda x < 1/4 şartı verilmişti burdan hareketle
x < 1/4
4x < 1 bulunur.
4x 1'den küçük olduğu için mutlak değerin içi negatif olur.
|4x - 1| = -1.(4x - 1) = 1 - 4x bulunur ve (1) ifadesinde yerine yazlırsa,
 1 - 4x - 2 = -4x -1
sonucuna ulaşılır.

Doğru Cevap B Seçeneğidir.


Turgut Arslan