Birim Hücre ve Wigner-Seitz Hücresi

Birim Hücrenin Tanımı Wigner-Seitz Hücresini Çizmek

İki boyutta 5 Bravais örgüsü

1. Kare örgü (a = b , = 90o)
2. Dikdörtgen Örgü (a b , = 90o)
3. Merkezli dikdörtgen örgü (rombik) (a b , = 90o)
4. Heksagonal (Üçgen) örgü (a = b , = 120o (60o))
5. Eğik Örgü (a b , 90o)

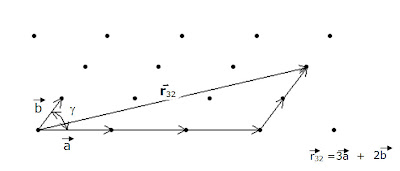
BİRİM HÜCRE: Şekilde gösterilen a ve b vektörleri ile oluşturan kapalı alanlar birim hücre, a ve b vektörleri birim hücre vektörleri olarak adlandırılır. ise a ve b vektörleri arasındaki açıdır. 3 boyutta ise c birim hücre vektörü de göz önüne alınmalıdır. 

PRİMİTİF (İLKEL) HÜCRE: En küçük hacimli ve tek örgü noktası içeren hücredir. Bir örgüdeki bütün mümkün primitif hücreler aynı hacme sahiptir. 2 boyutlu örgü tiplerinde gösterilen Kare, Dikdörtgen, Heksagonal ve Eğik örgüler primitif hücre, Merkezli dikdörtgen örgü ise primitive hücre değildir, çünkü iki örgü noktası içermektedir ve bu nedenle en küçük hacimli hücre değildir.

İki tip primitif hücre vardır. Biri; herbir en yakın örgü noktasının birim vektörlerle bir araya getirilerek oluşturulan ve köşelerindeki örgü noktalarının hücreye katkısı toplam 1 olan primitif hücre; diğeri ise bir örgü noktası ile en yakın komşularını birleştiren çizgileri dik olarak ortalarından kesen çizgilerin (3 boyutlu durumda düzlemlerin) oluşturduğu ve yalnızca merkezinde bir örgü noktası içeren Wigner-Seitz hücresi olarak adlandırılan hücredir.

Wigner-Seitz Hücresi Nasıl Çizilir?

	Bir örgü noktası seçin ve buna en yakın komşularını birleştiren çizgileri çizin.
	Çizgilere dik olan ve ortalarından geçen çizgileri çizin.
	En küçük kapalı  alan WIGNER-SEITZ PRİMİTİF HÜCRESİ dir.

Katı Hal Fiziği Ders Notları Sayfa 3

KRİSTALOGRAFİNİN TEMELLERİ

1. 1 KRİSTALOGRAFİNİN TEMELLERİ

Kristalografi Nedir?

Kristalografi; kristal yapısını inceleyen bilim dalıdır.  Herhangi bir kristalin hangi kristal yapıda olduğu kristalografik yöntemlerle belirlenir.

Kristal yapılar uygulanabilir SİMETRİ işlemlerine bağlı olarak türlerine göre sınıflandırılırlar.  Simetri işlemleri gayet iyi bir şekilde Grup Teori yönemleriyle incelenebilir.

Bu dersin içeriğinde basit yapıları ele alacağız ve Grup Teori’ye gereksinimimiz olmayacak.

1.2. ÖRGÜ ve BAZ

ÖRGÜ (LATİS): 3 boyutta periyodik olarak dizilmiş sonsuz noktalar topluluğudur. Her noktanın çevresi geometrik olarak bakıldığında özdeştir yani latis mükemmel öteleme simetrisine sahiptir. Bu sayede örgüdeki bütün noktalar  a, b  ve c birim vektörleriyle tanımlanabilir:

  

r = ua + vb+ wc       u, v, w tam sayıdır.

 Birim örgünün vektörlerden yararlanılarak oluşturulması

Bir katı cismin kristal yapıda olması için kesinlikle öteleme simetrisine sahip olması gerekir.

Doğada simetri işlemlerinin getirdiği kısıtlamalar nedeniyle Bravais (1845) örgüleri olarak adlandırılan 2 boyutta 5 ve 3 boyutta 14 örgü tipi bulunmaktadır.

 

İki boyutta 5 Bravais örgüsü

1. Kare örgü (a = b , = 90o)
2. Dikdörtgen Örgü (a b , = 90o)
3. Merkezli dikdörtgen örgü (rombik) (a b , = 90o)
4. Heksagonal (Üçgen) örgü (a = b , = 120o (60o))
5. Eğik Örgü (a b , 90o)

Katı Hal Fiziği Ders Notları Sayfa 2

Katı Cisimler ve Kristal Yapıları

KATI HAL FİZİĞİ I

I.BÖLÜM

      KRİSTAL YAPI

GİRİŞ

Katı Hal Fiziği; doğadaki katı cisimlerin fiziksel özelliklerini inceler. Son yıllarda “Yoğun Madde Fiziği” olarak adlandırılmasının temelinde bu fizik dalının sıvılar, sıvı metaller, sıvılaştırılmış gazlar, erimiş tuzlar, sıvı kristaller vb. konularını içermesi yer almaktadır.

Bu dersin içeriği yalnızca katı cisimler olacağı için Katı Hal Fiziği olarak adlandırılmaktadır.

Doğada katı cisimler, atomlarının yerleşimine göre 3’e ayrılırlar:

1. Kristal Katılar: Atomların düzenli olarak yerleştiği yapılardır.

2. Polikristal Katılar: Bölgesel olarak kristal yapılara sahiptirler ama bir bütün olarak bakıldığında tek kristal özelliği göstermezler.

3. Amorf (Düzensiz yapılar) Katılar: Atomları rastgele yerleşmiştir.