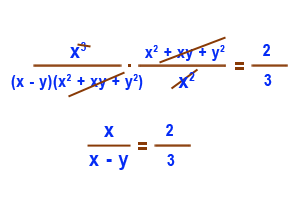İşçi Problemleri 2008 ALES İlkbahar Sayısal-1 Soru 3

SORU:

Ali bir işi Birol'ün 3 katı sürede tamamlayabilmektedir.
İkisi beraber aynı işin yarısını 3 günde tamamlayabiliyorlarsa Ali işin 3/4'ünü tek başına kaç günde yapar?(2008 ALES İlkbahar Sayısal-1)

A) 12   B) 15   C) 18   D) 21   E) 24

ÇÖZÜM:

Birolün işi tamamlama süresine X gün diyelim. Buna göre Ali'nin işi tamamlama süresi 3X olacaktır. İkisi beraber bir işin yarısını 3 günde, tamamını ise 6 günde yapmaktadırlar. şimdi bu hesaplamayı yapan denklemi kuralım,

1/3X + 1/X = 1/6
1/3X + 3/3X = 1/6
4/3X = 1/6 Buradan
X = 8 bulunur.
Ali bu işi 3 . 8 = 24 günde yapar.
Aynı işin 3/4'ünü ise
3/4 . 24 = 18 günde yapar

Doğru cevap C seçeneğidir.

Turgut Arslan

İşçi Problemleri 2008 ALES İlkbahar Sayısal-1 Soru 2

SORU:

Ahmet bir işin 2/3'ünü 8 saatte, İsmail aynı işin 1/6'sını 1 saatte yapmaktadır.
Buna göre ikisi beraber aynı işin yarısını kaç satte yaparlar?(2008ALES İlkbahar Sayısal-1)

A) 1,5   B) 2   C) 2,5   D) 3,5   E) 4

ÇÖZÜM:

Ahmet,

Bir işin 2/3'ünü 8 saatte tamamlarsa,
3/3'ünü(Tamamını) X saatte tamamlar(Doğru Orantı)

2/3 . X = 8 . 3/3

X = 12 saatte tamamlar.

İsmail,

Aynı işin 1/6'sını 1 saatte tamamlarsa,
6/6'sını(Tamamını) Y saatte tamamlar(Doğru Orantı)

1/6 . Y = 1 . 6/6

Y = 6 saatte tamamlar.

İkisi birlikte,

1/12 + 1/6 = 1/t

1/12 + 2/12 = 1/t

3/12 = 1/t

t = 4 saatte tamamın yaparlar

Yarsını ise 4/2 = 2 saatte yaparlar

Doğru cevap B seçeneğidir.

Turgut Arslan

Karışım Problemi 1999-3 KPSS Soru ve Çözümü

SORU:

Hacimce %25'i alkol olan 40 litrelik bir karışımdan 8 litre alınarak yerine 8 litre su ilave ediliyor.
Buna göre yeni karışımın hacimce alkol oranı yüzde kaçtır?(1999-3 KPSS Lisans)

A) 23   B) 22   C) 21   D) 20   E) 18

ÇÖZÜM:

Karışımdan 8 lt çıkarılırsa,
40 - 8 = 32 lt karışım kalır. Karışımdan madde almak karşımın oranını değiştirmez. 32 litrelik karışımın da %25'i alkoldür. Şimdi karışımdaki alkol miktarını bulalım,
32.(25/100) = 8 lt alkol miktarı.
Karışıma 8 litre saf su katıldığında alkol miktarı yine 8 lt olarak kalır ama karışımın hacmi değiştiği için alkol oranı düşecektir.
32 + 8 = 40 lt Karışımın son hacmi,
Karışımdaki alkol oaranı ise,
8/40 = 1/5' tir. Yüzdeyi hesaplamak için kesrin paydası 100'e genişletilmelidir. Kesrin değerinin değişmemesi için payı ve paydası 20 ile çarpılarak genişletilir.
Sonuç 20/100 Bulunur.
Yeni karışımdaki alkol oranı hacimce %20 dir.

Doğru cevap D seçeneğidir.

Turgut Arslan

Kolayca İngilizce Kelime Ezberlemek

Sayı Problemleri 2008 KPSS Soru ve Çözümü

SORU:

Bir sinema filminin biletleri öğrencilere 5 YTL'den diğer izleyicilere ise 8 YTL'den satılmıştır.
Bu film için satılan biletlerin sayısı 90 ve bilet satşından elde edilen para 510 YTL olduğuna göre, biletlerin kaç tanesi öğrencilere satılmıştır?(2008 KPSS)

A) 45   B) 50   C) 60   D) 70   E) 80

ÇÖZÜM:

Film için bilet alan öğrencilerin sayısı x olsun. Buna göre x kadar öğrenci 5x YTL para öder.

Toplamda 90 adet bilet satılmış. x tanesi öğrencilere satılmış ise 90 - x tanesi de diğer izleyicilere satılmıştır. Öğrenci olmayanların ödedikleri bilet parası 8(90 - x) YTL olur.

Toplamda 510 YTL ödenmiş. buna göre denklemimiz,

5x + 8(90 - x) = 510
5x + 720 - 8x = 510
3x = 210
x = 70

Toplamda 70 bilet öğrencilere satılmıştır.
Doğru Cevap D seçeneğidir

Turgut Arslan

Mutlak Değer 2008 KPSS Soru ve Çözümü

SORU:

a < a2 < |a|
eşitsizliğinin gerçeklenebilmesi için a aşağıdaki aralıkların hangisinde olmalıdır?(2008 KPSS)

A) (-∞, 1)   B) (-∞, 0)   C) (-1, 0)   D) (0, 1)   E) (0, +∞)

ÇÖZÜM:

İlk olarak eşitsizliğin en solundan incelemeye başlayalım,

a < a2

Bir sayının karesi kendisinden daima büyüktür buna göre a pozitif veya negatif herhangi bir sayı olabilir.

a2 < |a|

bir sayının karesinin, mutlak değerinden küçük olması için o sayının bir rasyonel(kesirli) sayı olması gerekir.

Örnek olarak a = 1/2 olsun,

(1/2)2 = 1/4

1/4 < |1/2|

a2 < |a|

eşitsizliği sağlanır.

Buraya dikkat!

Şimdiye kadar elde ettiğimiz verilerden yola çıkarak a'nın (0, 1) aralığında bir sayı olması gerektiği kanısına kapılabiliriz. Ancak şunu unutmayın henüz a'nın işaretini tam olarak belirlemedik!!!

Kesin olan tek bilgi a'nın rasyonel olduğudur. a'nın işaretini bulmak için yeniden eşitsizliğin el sol kısmına dönelim.

a < a2 eşitsizliği için artık a'nın rasyonel bir sayı olduğunu biliyoruz. Bildiğiniz gibi rasyonel sayılarda payda büyüdükçe sayı küçülür (Örn; 1/4 < 1/2). Bir rasyonel sayının karesinin kendisinden büyük olabilmesi için o sayının negatif olması gerekir.

Örneğin a = -1/2 olsun 

(-1/2)2 = 1/4

-1/2 < 1/4

Buna göre a = -1/2 için soruda verilen eşitsizliğin tüm şartlarını birleştirirsek,

-1/2 <(-1/2)2 < |-1/2| elde edilir. 

a < a2 < |a| olabilmesi için 

-1 < a < 0 aralığında olmalıdır.

Doğru Cevap C Seçeneğidir.

Turgut Arslan

Rasyonel Sayılar 2009 KPSS Soru ve Çözümü

SORU:

Olduğuna göre, x/y kaçtır?(2009 KPSS)

A) -3   B) -2   C) -1   D) 2   E) 3

ÇÖZÜM:

Rasyonel denklemler çözülürken, aritmetiksel işlemler rasyonel sayılarda olduğu gibi yapılır. İki rasyonel sayı birbirlerine bölünürken bölünen olduğu gibi kalırken bölen yani payda kısmı ters çevrilip bölenle yani pay kısmı ile çarpılır. sorudaki,

x3 - y3 ifadesi yani iki küp farkı açık şekilde yazılmıştır.

x3 - y3 = (x - y)(x2 + xy + y2)

gerekli sadeleştirmeler yapılır ve yukarıdaki eşitlik elde edilir. Ardından içler dışlar çarpımı yaılırsa,

3x = 2(x - y)

3x = 2x - 2y

x = -2y

x/y = -2 olarak bulunur.

Doğru Cevap B Seçeneğidir.

Turgut Arslan

Analitik Geometri 2009 KPSS Soru ve Çözümü

SORU:

Yukarıdaki dik koordinat sisteminde K(4,3) noktasından geçen doğru x eksenini apsisi a olan, y eksenini de ordinatı b olan noktalarda kesmektedir.
Buna göre (a - 4)(b - 3) çarpımının değeri kaçtır?(2009 KPSS)

A) 8   B) 12  C) 14  D) 16  E) 18

ÇÖZÜM:

Öncelikli olarak genel doğru denklemini yazalım.

   x  

x1 - x0

+

   y  

y1 - y0

= 1
Grafikteki verileri kullanarak doğru denklemimizi oluşturalım,

   x  

a - 0

+

   y  

b - 0

= 1
fizikliblog.blogspot.com

x

a

+

y

b

= 1 şimdi de paydaları eşitleyelim ve gerekli işlemleri yapalım
(b)    (a)
4b + 3a = ab olur. buradan,
ab - 4b - 3a = 0 bulunur.
(a - 4)(b - 3) Soruda verilen çarpım işlemini yaparsak,
ab - 4b - 3a + 12 elde edilir. burada yukarıda bulduğumuz ifadeyi yerine koyarsak,
0 + 12 = 12 olarak bulunur.
Doğru Cevap B Seçeneğidir.



Turgut Arslan

Pisagor Teoremi 2009 KPSS Soru ve Çözümü

SORU:

Aşağıdaki şekilde uç noktaları A ve D olan bir su bitkisinin durgun [OA] ve rüzgarlı havadaki [OD] konumu gösterilmiştir.

Buna göre x cm'dir?(2009 KPSS)

A) 25   B) 28   C) 30   D) 32   E) 35

ÇÖZÜM:

İlk olarak bitkinin boyunu hesaplayalım
|OA| = x + 5cm
aynı şekilde
|OD| = x + 5cm (bitkinin boyu sabittir.)
|OC| = |OD| - |CD|
|OC| = x + 5 - 3 = x + 2
OBC dik üçgeninde Pisagor Teoremi uygulanırsa,
x2 + 122 = (x + 2)2
x2 + 122 = x2 + 4x + 4
4x + 4 = 144
4x = 140
x = 35 cm bulunur.
Doğru Cevap E Seçeneğidir.



Turgut Arslan

Faktöriyel 2007 ALES Sonbahar Say-1 Soru ve Çözümü

SORU:

1.2.3.4.5......11.12

           2n

ifadesinde mümkün olan tüm sadleştirmeler yapılınca sonucun bir tam sayı olduğu görülüyor.
Buna göre n en fazla kaç olabilir?(2007 ALES Sonbahar Sayısal-1)
A) 7   B) 8   C) 9   D) 10   E) 12

ÇÖZÜM:

1.2.3.4.5......11.12

           2n

=

12!

2n

n sayısını bulabilmek için 12!'deki 2 çarpanlarının kaç tane olduğunu araştırılır. aşağıdaki bölme işlemi 1 sayısını elde edinceye kadar tekrarlanır. Bulunan bölümler toplanır. 

Bölüm değerleri toplanırsa,
6 + 3 + 1 = 10 bulunur. Doğru Cevap D Şıkkıdır


Turgut Arslan

Ardışık Sayılar 2008 ALES Sonbahar Say-2 Soru ve Çözümü

SORU:

n tek sayı olmak üzere, n tane adışık pozitif sayının toplamı, ortadaki sayı ile n çarpılarak bulunur. Bu ardışık çift saylar için de geçerlidir.
7 + 8 + 9 = 8x3 = 20
12 + 14 + 16 + 18 + 20 = 16x5 = 80
Buna göre 230 + 232 + ....... + 266 toplamı aşağıdaki çarpımların hangisine eşittir?(2008 ALES Sonbahar Sayısal-2)
A) 248x17   B) 248x19   C) 248x21   D) 250x17   E) 250x19

ÇÖZÜM:

İlk önce ardışık serideki terim sayısı bulunur.

 

Bir ardışık sayı dizisinde ortadaki terim, ilk ve son terimin toplamının yarısıdır.

Çarpım = 248x19 olur

Doğru Cevap B Seçeneğidir



Turgut Arslan

Sayılar 2007 ALES Sonbahar Sayısal-1 Soru ve Çözümü

SORU:

a ve b pozitif birer tam sayı olmak üzere,
3a + 5b = 300
eşitliğini sağlayan en büyük b değeri kaçtır?(2007 ALES Sonbahar Sayısal-1)
A) 57   B) 55   C) 53   D) 51   E) 49

ÇÖZÜM:

3a + 5b = 300 denklemde a'ya değerler vererek b'nin alabileceği değerler belirlenir. b pozitif bir tam sayı olarak tanımlandığı için b'yi tam sayı çıkaran a değerleri bulunmalıdır.
a = 5 için,
3 . 5 + 5b = 300
15 + 5b = 300
5b = 285
b = 57 olarak bulunur.
Doğru Cevap A Seçeneğidir.



Turgut Arslan

Sayılar Örnek Soru 3

SORU:

a, b ve c birbirlerinden farklı birer rakam olmak üzere,
8a - 5b + 2c
ifadesinin alabileceği en küçük tam sayı değeri nedir?

ÇÖZÜM:

a,b ve c birer rakam olduklarına göre alabilecekleri değerler kümesi şu şekildedir,
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9) bu kümeden soruda verilen denklemi en küçük yapmak üzere,
a = 0
b = 9
c = 1
Değerleri seçilirse sonuç,
8 . 0 + 5 . 9 + 2 . 1 = - 43 bulunur.



Turgut Arslan

İkinci Derece Denklemler Örnek Soru 1

SORU:

a ve b doğal sayılar olmak üzere,

a2 - b2 = 17

olduğuna göre a.b çarpımının değeri nedir?

ÇÖZÜM:

a2 - b2 = (a - b).(a + b) tam kare denklemi
a2 - b2 = 17 (a - b).(a + b) = 17 (17 asal sayıdır ve çarpanları 1 ve 17 dir.) buna göre,
a - b = 1
a + b = 17
2a = 18
a = 9
a'nın değeri denklemde yerine koyulur ve b bulunur
9 - b = 1
-b = 1 - 9
-b = -8
b = 8 olur.
Buna göre a.b çarpımı,
9.8 = 72 olarak bulunur.



Turgut Arslan

Sayılar Örnek Soru 2

SORU:

(7m - 3) ile (5m + 7) sayıları ardışık tek tam sayılardır. Buna göre m'nin alabileceği değerler toplamı nedir?

ÇÖZÜM:

iki ardışık tek tam sayı arasındaki fark 2'dir.Bu bilgiye istinaden bu iki tek tam sayıyı birbirinden çıkaralım. Ancak (7m - 3) ile (5m + 7)'den hangisinin büyük olduğu tam olarak bilinmediğinden dolayı her iki durum için de hesaplama yapmak gerekir.

Durum 1

(7m - 3) - (5m + 7) = 2

7m - 3 - 5m - 7 = 2

2m - 10 = 2

2m = 12 

m = 6

Durum 2

(5m + 7) - (7m - 3) = 2

5m + 7 - 7m + 3 = 2

-2m + 10 = 2

-2m = -8

m = 4

Her iki durum da toplanarak m için olabilir değerler toplamı bulunur.

6 + 4 = 10

Turgut Arslan

Sayılar 2008 ALES Sonbahar Say-1 Soru ve Çözümü

SORU:

x ve y birer doğal sayı olmak üzere,
y(x + 2) = 6
eşitliğini sağlayan x değerlerinin toplamı nedir?(2008 ALES Sonbahar Sayısal 1)
A) 3   B) 4   C) 5   D) 6   E) 7

ÇÖZÜM:

 y(x + 2) = 6 eşitliğinde  y'ye soruda verilen şarta uygun değerler verilir ve bu değerlere karşı gelen x sayıları bulunur.

y = 1 için x = 4

y = 2 için x = 1

y = 3 için x =0

y = 6 için x = -1  bu değeri alamaz çünkü x sorunun başında bir doğal sayı olarak tanımlanmıştı. 

Soruda verilen şartlara uygun x değerleri toplanırsa,

4 + 1 + 0 = 5 bulunur.

Doğru Cevap C Seçeneğidir.

Turgut Arslan

Sayılar 2007 ALES Sonbahar Say-1 Soru ve Çözümü

SORU:

a ve b pozitif tam sayıları için,

a

3

+ b = 8

olduğuna göre a'nın alabileceği en büyük değer kaçtır?(2007 ALES Sonbahar Sayısal-1) 

A) 27   B ) 24   C) 21   D) 18   E) 15

ÇÖZÜM:

 a'nın en büyük değerini alabilmesi için b en küçük olmalıdır. a ve b pozitif tam sayılar olduğu için b = 0 olamaz b > 0 dır. Buna göre b = 1 değerini alabilir. Bu durumda,

a

3

+ 1 = 8

a/3 = 7 olur. Buradan,

a = 3 . 7 = 21 bulunur.

Doğru Cevap C Seçeneğidir.



Turgut ARSLAN

Faktöriyel 2008 ALES İlkbahar Say 2 Soru ve Çözümü

SORU:

10!

2m

= a
olduğuna göre m'nin alabileceği en büyük değer kaçtır?(2008 ALES İlkbahar Sayısal 2)
A) 5   B) 6   C) 7   D) 8   E) 9

ÇÖZÜM:

10!

2m

= a
ifadesinde içler dışlar çarpımı yaparsak,
10! = 2m.a eşitliğini elde ederiz. Bu eşitlikte m'nin alabileceği en buyük değeri bulabilmek için 10! içinde kaç adet 2 bulunduğuna bakılır,

Elde edilen bölüm değerleri toplanırsa 10! içindeki 2 çarpanlarının sayısı bulunur,
5 + 2 + 1 = 8

Doğru Cevap D Seçeneğidir.





Turgut Arslan

Faktöriyel Örnek Soru 2

SORU:

(a + 1)!

(b - 1)!

= 24 eşitliğini sağlayan a + b ifadesinin alabileceği değerler toplamı kaçtır?

ÇÖZÜM:

(a + 1)!

(b - 1)!

= 24

1. Durum

(a + 1)! = 24.(b - 1)!     (b - 1)! = 23! olarak düşünülebilir. Bu durumda ifademiz,
(a + 1)! = 24.23! = 24! olur
a + 1 = 24 => a = 23
b - 1 = 23 => b = 24
a + b = 23 + 24 = 47 olur.

2. Durum

(a + 1)! = 24.(b - 1)! = 4.3.(b - 1)!     (b - 1)! = 2! olarak düşünülebilir. Bu durumda ifademiz,
(a + 1)! = 4.3.2! = 4! olur.
a + 1 = 4 => a = 3
b - 1 = 2 => b = 3
a + b = 3 + 3 = 6 olur.

3. Durum

(a + 1)!

(b - 1)!

= 4!/0!
a + 1 = 4 => a = 3
b - 1 = 0 => b = 1
a + b = 3 + 1 = 4 olur.
Olası 3 durumun toplamı a + b ifadesinin alabileceği değerler toplamını verir.
1. Durum + 2. Durum + 3. Durum
47 + 6 + 4 = 57 bulunur.



Turgut ARSLAN

Sayılar Basamak Kavramı 2007 ALES Sonbahar Say-1 Soru ve Çözümü

SORU:

Üç basamaklı 8AB sayısı iki basamaklı AB sayısının 33 katı olduğuna göre A + B kaçtır?(2007 ALES Sonbahar Sayısal-1)
A) 3    B) 5   C) 6   D) 7   E) 9

ÇÖZÜM:

8AB = 33(AB)
800 + AB = 33(AB)
800 = 32(AB)
AB = 800/32 = 25
A = 2
B = 5
A + B = 2 + 5 = 7

Doğru Cevap D Seçeneğidir.


Turgut Arslan

Hareket Problemleri 2009 KPSS Soru ve Çözümü

SORU:

Bir deniz motoru |AB| yolunu saatte (v + 20)km hızla 24 dakikada, aynı yolu saatte (v - 6)km hızla 32 dakikada alıyor.
Buna göre |AB| yolu kaç km'dir?(2009 KPSS)
A) 40,2   B) 40,8   C) 41,2   D) 41,6   E) 41,8

ÇÖZÜM:

|AB| yolu x km olsun, soruda hızlar saat cinsinden verildiği için dakikaları saate çevirelim
60 dakika 1 saat ise
24 dakika y saat eder (Doğru orantı)

60y = 24
y = 24/60 = 2/5 saat

60 dakika 1 saat ise
32 dakika y saat eder (Doğru orantı)

60y = 32
y = 32/60 = 8/15 saat

Yol = Hız . Zaman Formülünden yola çıkarak x km için iki farklı ifade yazılabilir.

x = (v + 20). 2/5
x = (v - 8) . 8/15

(v + 20). 2/5 = (v - 8) . 8/15
(v + 20) = (v - 8). 4/3 buradan,
6v + 120 = 8v - 48
2v = 168
v = 84 km/h olur.
Bu değeri x için yazılan denklemlerden birinde yerine koyarsak |AB| yolunu hesaplayabiliriz
x = (84 + 20). 2/5
x = 41,6 km bulunur.

Doğru Cevap D Seçeneğidir.



Turgut Arslan