Faktöriyel 2007 ALES Sonbahar Say-1 Soru ve Çözümü

SORU:

1.2.3.4.5......11.12

           2n

ifadesinde mümkün olan tüm sadleştirmeler yapılınca sonucun bir tam sayı olduğu görülüyor.
Buna göre n en fazla kaç olabilir?(2007 ALES Sonbahar Sayısal-1)
A) 7   B) 8   C) 9   D) 10   E) 12

ÇÖZÜM:

1.2.3.4.5......11.12

           2n

=

12!

2n

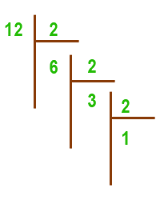
n sayısını bulabilmek için 12!'deki 2 çarpanlarının kaç tane olduğunu araştırılır. aşağıdaki bölme işlemi 1 sayısını elde edinceye kadar tekrarlanır. Bulunan bölümler toplanır. 

Bölüm değerleri toplanırsa,
6 + 3 + 1 = 10 bulunur. Doğru Cevap D Şıkkıdır


Turgut Arslan

Faktöriyel 2008 ALES İlkbahar Say 2 Soru ve Çözümü

SORU:

10!

2m

= a
olduğuna göre m'nin alabileceği en büyük değer kaçtır?(2008 ALES İlkbahar Sayısal 2)
A) 5   B) 6   C) 7   D) 8   E) 9

ÇÖZÜM:

10!

2m

= a
ifadesinde içler dışlar çarpımı yaparsak,
10! = 2m.a eşitliğini elde ederiz. Bu eşitlikte m'nin alabileceği en buyük değeri bulabilmek için 10! içinde kaç adet 2 bulunduğuna bakılır,

Elde edilen bölüm değerleri toplanırsa 10! içindeki 2 çarpanlarının sayısı bulunur,
5 + 2 + 1 = 8

Doğru Cevap D Seçeneğidir.





Turgut Arslan

Faktöriyel Örnek Soru 2

SORU:

(a + 1)!

(b - 1)!

= 24 eşitliğini sağlayan a + b ifadesinin alabileceği değerler toplamı kaçtır?

ÇÖZÜM:

(a + 1)!

(b - 1)!

= 24

1. Durum

(a + 1)! = 24.(b - 1)!     (b - 1)! = 23! olarak düşünülebilir. Bu durumda ifademiz,
(a + 1)! = 24.23! = 24! olur
a + 1 = 24 => a = 23
b - 1 = 23 => b = 24
a + b = 23 + 24 = 47 olur.

2. Durum

(a + 1)! = 24.(b - 1)! = 4.3.(b - 1)!     (b - 1)! = 2! olarak düşünülebilir. Bu durumda ifademiz,
(a + 1)! = 4.3.2! = 4! olur.
a + 1 = 4 => a = 3
b - 1 = 2 => b = 3
a + b = 3 + 3 = 6 olur.

3. Durum

(a + 1)!

(b - 1)!

= 4!/0!
a + 1 = 4 => a = 3
b - 1 = 0 => b = 1
a + b = 3 + 1 = 4 olur.
Olası 3 durumun toplamı a + b ifadesinin alabileceği değerler toplamını verir.
1. Durum + 2. Durum + 3. Durum
47 + 6 + 4 = 57 bulunur.



Turgut ARSLAN

Faktöriyel Örnek Soru 1

SORU:

(n+1)! / (n-1)! =6 ise n nedir?

ÇÖZÜM:

(n+1)! / (n-1)! =6 denkleminde paydaki (n + 1)! ifadesini (n - 1)!'e kadar açalım.
(n+1).(n).(n-1)! /(n-1)!  = 6
n.(n+1) = 6
n2 + n - 6 = 0 şeklinde bir ikinci dereceden denklem elde ederiz. Şimdi bu denklemi çözelim.
n           -2   denklem çarpanlarına ayrılır.
n            3

(n-2).(n+3) = 0 ise (n-2) = 0 ve (n + 3) = 0 olur buna göre
n = 2 ve n = -3 bulunur.

Denklemin çözüm kümesi Ç = {-3, 2} olur.



Turgut Arslan

Faktöriyel Kavramı ( n! )

Faktöriyel aslında özel bir çarpım serisidir. n pozitif bir doğal sayı olmak üzere, 1'den n'ye kadar olan sayıların çarpımı n! şeklinde gösterilir.

Faktöriyelin en genel ifadesi

n!= 1.2.3.4.5...........(n - 1).n

şeklindedir.

Faktöriyel 2009 KPSS Soru ve Çözümü

Soru:

a ve k pozitif tam sayılar olmak üzere 

6! = 2k.a

eşitliğinde k en büyük değerini aldığında a kaç olur?  (2009 KPSS)
 A) 15   B) 25   C) 30   D) 45   E) 60

Çözüm:

6! = 2k.a  denkleminin sol tarafını sağ tarafına benzetmeye çalışalım. Bunun için ilk önce 6!'i açık olarak yazalım.

6.5.4.3.2.1 = 2k.a  sol taraftaki 6 ve 4 sayılarını da 2'nin çarpanları şeklinde açalım.

2.3.2.2.3.2.1=2k.a  2'leri bir araya getirelim.

24.3.5.3=2k.a bu eşitliğe göre k'nın en büyük değeri sol tarafta 2'li terimin üssü olan 4 tür. Diğer sayılar çarpılarak k'nın en büyük değeri için a sayısı bulunur.

a = 3.3.5

a = 45 Doğru Cevap D seçeneğidir.